NOTASI ILMIAH
by:Fiko Arif
by:Fiko Arif
Notasi Ilmiah
Notasi ilmiah adalah cara penulisan nomor yang mengakomodasi nilai-nilai terlalu besar atau kecil untuk dengan mudah ditulis dalam notasi desimal standar. Notasi ilmiah memiliki sejumlah sifat yang berguna dan umumnya digunakan dalam kalkulator, dan oleh para ilmuwan, matematikawan, dokter, dan insinyur.
Dalam notasi ilmiah, semua nomor ditulis seperti ini:
Notasi Ilmiah. Menurut aturan notasi ilmiah hasil pengukuran dapat dituliskan
a,…x 10n
a = bilangan asli 1 sampai 9
n = bilangan eksponen
n = bilangan eksponen
Dalam notasi ilmiah
hasil pengukuran harus dinyatakan dalam 1 angka di depan koma. Angka
125 jika kita tuliskan dalam bentuk baku (notasi ilmiah) menjadi 1,2 x
102.
Penulisan dengan Notasi Ilmiah
Untuk menuliskan hasil pengukuran ke
dalam bentuk notasi ilmiah cukup mudah. Anda cukup melihat apakah
bilangan tersebut lebih dari 10 atau kurang dari 1.
Notasi Ilmiah untuk Bilangan Lebih dari 10, caranya:
- Jika bilangan yang lebih dari 10 tidak mempunyai koma (bukan desimal) buatlah koma di belakang angka paling belakang. Jika bilangan tesebut telah memiliki koma sobat tidak perlu menambahkannya lagi.
- Buatlah koma di sebelah kanan angka pertama.
- Hilangkanlah angka nol di belakang koma selain yang diapit angka bukan nol
- Kalikan bilangan yg sobat dapat di angka 3 dengan 10n, dimana n = jumlah angka yang diapit dua koma.
105.000.000.000.000
(angka yang akan kita nyatakan dalam notasi ilmiah)\
105.000.000.000.000, (kita taruh koma dibelakang angka terakhir [warna merah])1,05.000.000.000.000, (buat koma dibelakang angka pertama [warna biru])
1,05 x 1014dimana 14 adalah jumlah angka yang diapit tanda koma pada langkah sebelumnya [warna orange].
contoh lainnya
135,2781,35,278
1,35278 x 102
Notasi Ilmiah untuk Bilangan Kurang dari 1, caranya:
- Buatlah koma di belakang angka pertama bukan nol yang sobat jumpai dari sebelah kiri
- Hilangkan angka dibelakang angka pertama yang sobat jumpai (langkah 1)
- Kalikan angka di nomor 2 dengan 10-n dengan n = jumlah angka yang diapit koma.
0,00001276
0,00001,276
0,00001,276
(buat koma di belakang angka bukan nol yang dijumpai pertama dari kiri)
1,276 x 10-5
1,276 x 10-5
Soal latihan
Nyatakan nilai besaran berikut dalam bentuk notasi ilmiah
a. 0,00008765 mb. 12.980.000.000 kg
c. 0,12000000234000 liter
c. 0,12000000234000 liter
MATEMATIKA
Bilangan Pangkat
By:Yoga Prayudi
1. Bilangan Berpangkat Sederhana
Dalam kehidupan sehari-hari kita sering menemui perkalian bilangan-bilangan dengan faktor-faktor yang sama. Misalkan kita temui perkalian bilangan-bilangan sebagai berikut.
Perkalian bilangan-bilangan dengan faktor-faktor yang sama seperti di atas, disebut sebagai perkalian berulang. Setiap perkalian berulang dapat dituliskan secara ringkas dengan menggunakan notasi bilangan berpangkat. Perkalian bilanganbilangan di atas dapat kita tuliskan dengan:
Bilangan 23, 35, 66 disebut bilangan berpangkat sebenarnya karena bilangan-bilangan tersebut dapat dinyatakan dalam bentuk perkalian berulang. Bilangan berpangkat an dengan n bilangan bulat positif didefinisikan sebagai berikut.
2. Bilangan Berpangkat Negatif
Apa yang terjadi jika m = 0? Dari pembahasan di atas jika dipilih m = 0, maka:
B. Bilangan Pecahan Berpangkat
Untuk menentukan hasil pemangkatan bilangan pecahan berpangkat dapat di gunakan definisi bilangan berpangkat. Jika a, b∈ B, b ≠ 0, n adalah bilangan bulat positif maka:
C. Bentuk Akar
Dalam matematika kita mengenal berbagai jenis bilangan. Beberapa contoh jenis bilangan diantaranya adalah bilangan rasional dan irrasional. Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk , dengan m, n ∈ B dan n ≠ 0. Contoh bilangan rasional seperti: , 5, 3 dan seterusnya. Sedangkan bilangan irrasional adalah bilangan riil yang tidak dapat dinyatakan dalam bentuk , dengan m, n ∈ B dan n ≠ 0. Bilangan-bilangan seperti termasuk bilangan irrasional, karena hasil akar dari bilangan tersebut bukan merupakan bilangan rasional.
Bilangan-bilangan semacam itu disebut bentuk akar. Sehingga dapat disimpulkan bahwa bentuk akar adalah akar-akar dari suatu bilangan riil positif, yang hasilnya merupakan bilangan irrasional.
1. Operasi Hitung Bentuk Akar
Dua bilangan bentuk akar atau lebih dapat dijumlahkan, dikurangkan, maupun dikalikan.
a. Penjumlahan dan Pengurangan Bentuk Akar
Untuk memahami cara menjumlahkan dan mengurangkan bilangan-bilangan dalam bentuk akar, perhatikan contoh – contoh berikut.
Dari contoh di atas, maka untuk menjumlahkan dan mengurangkan bilangan-bilangan dalam bentuk akar dapat dirumuskan sebagai berikut. Untuk setiap a, b, dan c bilangan rasional positif, berlaku hubungan:
b. Perkalian Bentuk Akar
Untuk sembarang bilangan bulat positif a dan b berlaku sifat perkalian berikut.
Sifat di atas sekaligus dapat digunakan untuk menyederhanakan bentuk akar.
c. Pemangkatan Bilangan Bentuk Akar
Bentuk akar juga dapat dipangkatkan. Adapun pemangtkatan bentuk akar akar didapat beberapa sifat.
2) Pemangkatan bentuk dengan pangkat negatif
Bentuk akar dengan pangkat negatif sama halnya dengan bilangan berpangkat bilangan negatif. Sehingga:
2. Hubungan Bentuk Akar dengan Pangkat Pecahan
Pada pembahasan yang lalu telah disebutkan beberapa sifat dari bilangan berpangkat bulat positif. Sifat-sifat tersebut akan digunakan untuk mencari hubungan antara bentuk akar dengan pangkat pecahan. Sifat yang dimaksud adalah .
Selain sifat tersebut terdapat sifat lain, yaitu:Jika ap = aq maka p = q dengan a > 0, a ≠ 1
a. Hubungan dengan
Perhatikan pembahasan berikut.
Dari uraian di atas dapat disimpulkan bahwa untuk a bilangan real tidak nol dan n bilangan bulat positif, maka:
D. Merasionalkan Bentuk Akar Kuadrat
Dalam sebuah bilangan pecahan penyebutnya dapat berupa bentuk akar. Pecahan adalah beberapa contoh pecahan yang penyebutnya berbentuk akar. Penyebut pecahan seperti itu dapat dirasionalkan. Cara merasionalkan penyebut suatu pecahan tergantung dari bentuk pecahan tersebut.
1. Merasionalkan Bentuk
Untuk menghitung nilai ada cara yang lebih mudah daripada harus membagi 6 dengan nilai pendekatan dari 3, yaitu dengan merasionalkan penyebut. Cara ini dapat dilakukan dengan menggunakan sifat perkalian bentuk akar:
Selanjutnya pecahan diubah bentuknya dengan memanipulasi aljabar.
2. Merasionalkan Bentuk
About these ads
By:Yoga Prayudi
BILANGAN BERPANGKAT DAN BENTUK AKAR
Dalam kehidupan sehari-hari kita sering menemui perkalian bilangan-bilangan dengan faktor-faktor yang sama. Misalkan kita temui perkalian bilangan-bilangan sebagai berikut.
Perkalian bilangan-bilangan dengan faktor-faktor yang sama seperti di atas, disebut sebagai perkalian berulang. Setiap perkalian berulang dapat dituliskan secara ringkas dengan menggunakan notasi bilangan berpangkat. Perkalian bilanganbilangan di atas dapat kita tuliskan dengan:
Bilangan 23, 35, 66 disebut bilangan berpangkat sebenarnya karena bilangan-bilangan tersebut dapat dinyatakan dalam bentuk perkalian berulang. Bilangan berpangkat an dengan n bilangan bulat positif didefinisikan sebagai berikut.
2. Bilangan Berpangkat Negatif
Apa yang terjadi jika m = 0? Dari pembahasan di atas jika dipilih m = 0, maka:
B. Bilangan Pecahan Berpangkat
Untuk menentukan hasil pemangkatan bilangan pecahan berpangkat dapat di gunakan definisi bilangan berpangkat. Jika a, b∈ B, b ≠ 0, n adalah bilangan bulat positif maka:
C. Bentuk Akar
Dalam matematika kita mengenal berbagai jenis bilangan. Beberapa contoh jenis bilangan diantaranya adalah bilangan rasional dan irrasional. Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk , dengan m, n ∈ B dan n ≠ 0. Contoh bilangan rasional seperti: , 5, 3 dan seterusnya. Sedangkan bilangan irrasional adalah bilangan riil yang tidak dapat dinyatakan dalam bentuk , dengan m, n ∈ B dan n ≠ 0. Bilangan-bilangan seperti termasuk bilangan irrasional, karena hasil akar dari bilangan tersebut bukan merupakan bilangan rasional.
Bilangan-bilangan semacam itu disebut bentuk akar. Sehingga dapat disimpulkan bahwa bentuk akar adalah akar-akar dari suatu bilangan riil positif, yang hasilnya merupakan bilangan irrasional.
1. Operasi Hitung Bentuk Akar
Dua bilangan bentuk akar atau lebih dapat dijumlahkan, dikurangkan, maupun dikalikan.
a. Penjumlahan dan Pengurangan Bentuk Akar
Untuk memahami cara menjumlahkan dan mengurangkan bilangan-bilangan dalam bentuk akar, perhatikan contoh – contoh berikut.
Dari contoh di atas, maka untuk menjumlahkan dan mengurangkan bilangan-bilangan dalam bentuk akar dapat dirumuskan sebagai berikut. Untuk setiap a, b, dan c bilangan rasional positif, berlaku hubungan:
b. Perkalian Bentuk Akar
Untuk sembarang bilangan bulat positif a dan b berlaku sifat perkalian berikut.
Sifat di atas sekaligus dapat digunakan untuk menyederhanakan bentuk akar.
c. Pemangkatan Bilangan Bentuk Akar
Bentuk akar juga dapat dipangkatkan. Adapun pemangtkatan bentuk akar akar didapat beberapa sifat.
2) Pemangkatan bentuk dengan pangkat negatif
Bentuk akar dengan pangkat negatif sama halnya dengan bilangan berpangkat bilangan negatif. Sehingga:
2. Hubungan Bentuk Akar dengan Pangkat Pecahan
Pada pembahasan yang lalu telah disebutkan beberapa sifat dari bilangan berpangkat bulat positif. Sifat-sifat tersebut akan digunakan untuk mencari hubungan antara bentuk akar dengan pangkat pecahan. Sifat yang dimaksud adalah .
Selain sifat tersebut terdapat sifat lain, yaitu:Jika ap = aq maka p = q dengan a > 0, a ≠ 1
a. Hubungan dengan
Perhatikan pembahasan berikut.
Dari uraian di atas dapat disimpulkan bahwa untuk a bilangan real tidak nol dan n bilangan bulat positif, maka:
D. Merasionalkan Bentuk Akar Kuadrat
Dalam sebuah bilangan pecahan penyebutnya dapat berupa bentuk akar. Pecahan adalah beberapa contoh pecahan yang penyebutnya berbentuk akar. Penyebut pecahan seperti itu dapat dirasionalkan. Cara merasionalkan penyebut suatu pecahan tergantung dari bentuk pecahan tersebut.
1. Merasionalkan Bentuk
Untuk menghitung nilai ada cara yang lebih mudah daripada harus membagi 6 dengan nilai pendekatan dari 3, yaitu dengan merasionalkan penyebut. Cara ini dapat dilakukan dengan menggunakan sifat perkalian bentuk akar:
Selanjutnya pecahan diubah bentuknya dengan memanipulasi aljabar.
2. Merasionalkan Bentuk
About these ads
Langganan:
Entri (Atom)
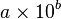
Tidak ada komentar:
Posting Komentar