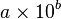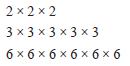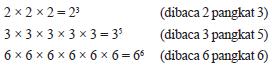HUKUM III NEWTON • HUKUM INI SERING JUGA DISEBUT DENGAN HUKUM AKSI-REAKSI. HUKUM INI BERBUNYI “JIKA SUATU BENDA MENGERJAKAN GAYA PADA BENDA LAIN MAKA BENDA YANG DI KENAI GAYA AKAN MENGERJAKAN GAYA YANG BESARNYA SAMA DENGAN GAYA YANG DI TERIMA DARI BENDA PERTAMA TETAPI ARAHNYA BERLAWANAN”. • PENERAPANNYA: – ADANYA GAYA GRAVITASI – PERISTIWA GAYA MAGNET – GAYA LISTRIK
·
· 9. APLIKASI HUKUM III NEWTON DALAM KEHIDUPAN SEHARI- HARI
· • 1 SESEORANG MEMAKAI SEPATU RODA DAN BERDIRI MENGHADAP TEMBOK. JIKA ORANG TERSEBUT MENDORONG TEMBOK (AKSI), MAKA TEMBOK MENDORONGNYA DENGAN ARAH GAYA YANG BERLAWANAN(REAKSI).
·  • 2. KETIKA MENEKAN UJUNG MEJA DENGAN TANGAN, TANGAN KITA MENGERJAKAN GAYA PADA MEJA(AKSI). DAN SEBALIKNYA UJUNG MEJA PUN MENEKAN TANGAN KITA(REAKSI).
• 2. KETIKA MENEKAN UJUNG MEJA DENGAN TANGAN, TANGAN KITA MENGERJAKAN GAYA PADA MEJA(AKSI). DAN SEBALIKNYA UJUNG MEJA PUN MENEKAN TANGAN KITA(REAKSI).
·  • 3. KETIKA KAKI PELARI MENOLAK PAPAN START KE BELAKANG(AKSI), PAPAN START MENDORONG PELARI KE DEPAN(REAKSI) SEHINGGA PELARI DAPAT MELAJU KE DEPAN.
• 3. KETIKA KAKI PELARI MENOLAK PAPAN START KE BELAKANG(AKSI), PAPAN START MENDORONG PELARI KE DEPAN(REAKSI) SEHINGGA PELARI DAPAT MELAJU KE DEPAN.
· 4. KETIKA SEORANG PERENANG MENGGUNAKAN KAKI DAN TANGANNYA UNTUK MENDORONG AIR KE BELAKANG(AKSI), AIR JUGA AKAN MENDORONG KAKI DAN TANGAN PERENANG KE DEPAN(REAKSI). •
·  5. KETIKA KITA BERJALAN DI ATAS TANAH, TELAPAK KAKI KITA MENDORONG TANAH KE BELAKANG. SEBAGAI REAKSI, TANAH MENDORONG KAKI KITA KE DEPAN SEHINGGA KITA DAPAT BERJALAN. •
5. KETIKA KITA BERJALAN DI ATAS TANAH, TELAPAK KAKI KITA MENDORONG TANAH KE BELAKANG. SEBAGAI REAKSI, TANAH MENDORONG KAKI KITA KE DEPAN SEHINGGA KITA DAPAT BERJALAN. •
·  6. KETIKA KITA MENEMBAK, SENAPAN MENDORONG PELURU KE DEPAN(AKSI). SEBAGAI REAKSI, PELURU PUN MENDORONG SENAPAN KE BELAKANG. •
6. KETIKA KITA MENEMBAK, SENAPAN MENDORONG PELURU KE DEPAN(AKSI). SEBAGAI REAKSI, PELURU PUN MENDORONG SENAPAN KE BELAKANG. •
· 7. KETIKA MENDAYUNG PERAHU, PADA WAKTU MENGAYUNKAN DAYUNG, PENDAYUNG MENDORONG AIR KE BELAKANG(AKSI). SEBAGAI REAKSI, AIR MEMBERI GAYA PADA DAYUNG KE DEPAN, SEHINGGA PERAHU BERGERAK KE DEPAN.
·
· 10. PENERAPAN HUKUM NEWTON PADA BERBAGAI KASUS • A. BENDA DI GANTUNG DENGAN TALI DAN DIGERAKKAN • DIGERAKKAN KE ATAS DENGAN PERCEPATAN A, MAKA: • • ::: GAYA YANG SEARAH DENGAN GERAK BENDA BERNILAI POSITIF ::: GAYA YANG BERLAWANAN DENGAN GERAK BENDA BERNILAI NEGATIF , SEHINGGA BERLAKU ∑F = M.A T-MG = M.A T = MG + MA • BENDA DIGERAKKAN KE BAWAH DENGAN PERCEPATAN A, MAKA: • :: GAYA YANG SEARAH DENGAN GERAK BENDA BERNILAI POSITIF DAN YANG BERLAWANAN BERNILAI NEGATIF RUMUS TEGANGAN TALINYA • ∑F = M.A MG – T = M.A T = MG-MA = M (G-A)
·





.jpg)



.jpg)


.jpg)